ART 025, SEP 2013
Music review — Federal University of Bahia
The Cantor Set as the Basis for the Compositional Design of “Pó”
Liduino Pitombeira
[email protected] – Universidade Federal do Rio de Janeiro
Maria di Cavalcanti
[email protected] – Universidade Federal de Campina Grande
Abstract
The fractal prototype known as Cantor Set, introduced by German mathematician Georg Cantor, in 1883, is the inspiration for the piece Pó, for piano, by Brazilian composer Liduino Pitombeira (b. 1962). The title Pó, the Portuguese word for dust, comes from Cantor Dust, which is the multidimensional version of this set formed by the Cartesian product of the set with itself. Articulations of the gestures as well as textural density, contour, and vertical distributions are representations—sometimes in strict fashion, other times in free fashion—of this beautiful geometric structure. This article intends to present and analyze Pitombeira’s Pó.
Although music’s foundations in Pythagorean mathematics have long been acknowledged, the active role played by mathematical procedures in the art of musical composition has varied over time. Throughout the Middle Ages and into the seventeenth century, music was grouped with arithmetic, geometry, and astronomy as a component of the quadrivium, the branch of liberal arts devoted to the exploration of numbers in terms of space and time. Towards the middle of the seventeenth century, however, composers and thinkers became increasingly interested in music’s relationship to the trivium, the branch of liberal arts that included grammar, logic, and rhetoric, and which served as a broader point of entry to the study of the more highly technical quadrivium. Johann Mattheson’s Der vollkommene Capellmeister (1739), for instance, makes a strong case for the application of rhetorical devices to the art of musical composition. Tides turned once again during the twentieth century as composers and theorists alike returned their attention to relationships between music and mathematics. Today, even a cursory perusal of significant music theory journals will reveal a large number of articles that refer to mathematics and geometry as tools for composition and analysis.
“Pó” (2008), a solo piano work that takes its name from the Portuguese word for dust, is an example of a composition based explicitly on mathematical processes. The design of “Pó” is based on the geometric structure known as the Cantor Set (figure 1). More specifically, “Pó” is designed after the Cantor ternary set, which is created by repeatedly deleting the middle thirds of a set of line segments until those segments become as small as dust grains (hence the title of the piece). This geometric structure was introduced in 1883 by the Russian-born German mathematician Georg Cantor (1845-1918), although it was also discovered by other mathematicians at around the same time. The graph is remarkable for its self-similarity, a property by which the same pattern will replicate on an increasingly small scale: the original image will be found in progressively smaller repetitions of that image. Self-similarity most often occurs in graphs produced by non-linear systems and fractals, such as the Mandelbrot Set. The process of continually removing the middle segments of lines generates the number series 1, 2, 4, 8, 6, 32, etc.

Figure 1. The Cantor Set
Pó is by no means the first piece of music to draw on the Cantor Set as the basis for its construction. Solomon (2009) traces structural affinities with the Cantor Set as far back as Beethoven’s Eccosaise in E-flat major, WoO83 (1806). More recently, Spanish composer Francisco Lara’s “Dust,” for chamber orchestra, draws on the Cantor Set for the definition of its form and melodic lines. Dr. Lara kindly provided us with a copy of his beautiful composition, which was awarded First Prize in the 2003 International Luxembourg Composition Prize.
One concern during the planning of Pó involved the representation of a spatial structure (the Cantor Set) in a temporal domain (successive musical events). Whereas objects of visual art are perceived in the dimension of space, music and other performing arts are perceived in time. As Robert Erickson pointed out (1963, 74), “our sense of time depends primarily upon the mental faculties of memory and attention.” By extension, our sense of time is inseparable from the idea of sequence. In Pó, therefore, the spatial construct of Cantor Set is communicated as a sequence of musical events, one after the other. Consequently, the listener’s musical memory allows him or her to visualize the gradual disclosure of the Cantor Set’s image (figure 1). At the same time, both complete and incomplete versions of the set’s spatial design can be found throughout the score. Through repeated listening and a good musical memory, the listener who has seen the score may eventually transfer those visual references to the Cantor Set into auditory references as well.
Another concern was related to the type of musical parameters to be used in the piece. The very nature of the instrument itself was essential for this decision. As the piano works primarily in chromatic space, with respect to pitch, the twelve notes of the chromatic scale were used as the basic materials for Pó. Coincidentally, number 12 is a multiple of two, three, four, and six, which makes it easier to construct the several layers of the Cantor Set. Therefore, the first organization of materials in the pitch domain consisted of defining a twelve-tone row, of which the different forms would be used as line segments of different sizes. The set itself inspired the choice for the basic cell that originated the entire row. The idea was to create a derived twelve-note row from a tetrachord, since a pitch-class set of this size can equally divide a row in three segments, which is the basic principle of constructing a Cantor Set.
If one takes the chromatic scale in ascending order and removes its four middle pitch-classes, the two remaining sets will both have prime form 0123. Even though it is possible to build a derived row from this tetrachord, since it does not have the interval class 4 within it, a more asymmetrical procedure was chosen, producing a tetrachord which has more closely related characteristics, at least as a representation, to the Cantor Set. As we have shown previously, for its property of self-similarity, the Cantor Set can be considered a fractal. The row-generator tetrachord was selected by the following procedure: from the first eight pitch-classes of a chromatic scale in ascending order (01234567), one removes the four middle elements, thus yielding the tetrachord with prime form 0167. This tetrachord (and also 0268 and 0369) has self-similarity because all of its subsets of three pitch-classes belong to the same set class, 016, which also has, according to a formula suggested by Isaacson (1991,11), the highest degree of similarity with its superset (0167). It would also be possible to generate another tetrachord by taking the first six pitch-classes of an ascending chromatic scale (012345), removing its two middle elements, thus producing the tetrachord 0145. Unfortunately, this tetrachord cannot generate a derived twelve-tone row, since it has occurrences of interval class 4 within its interval vector (201210). Figure 2 shows the twelve-tone matrix created from a twelve-tone row, in which all the tetrachords have prime form 0167. The hexachords of this row have both prime form 012678, which has level 2 combinatoriality. This fact means that for each form of the row it is possible to find two other rows in either P, R, I, or RI formats that produce combinatoriality.
Many gestures built from the matrix and texturally designed to convey temporal and spatial representations of the Cantor Set were applied throughout the piece. In fact, the formal design of the work consists primarily of the juxtaposition of these gestures so as to recall the very geometry of the Set. Several musical gestures of Pó attest to this formal underpinning. In the gesture shown in Figure 3, for example, the twelve tone row RI4 appears initially in the left hand of the piano and is repeated four times as rows RI0 and RI8 are juxtaposed on top of it with their middle pitch-classes removed. The drawing is not made in the natural order of fragmentation, that is, the intermediate level appears later, thus revealing the picture just in the last four measures.
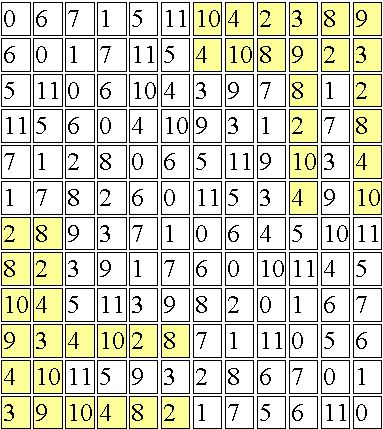
Figure 2. The twelve-tone matrix
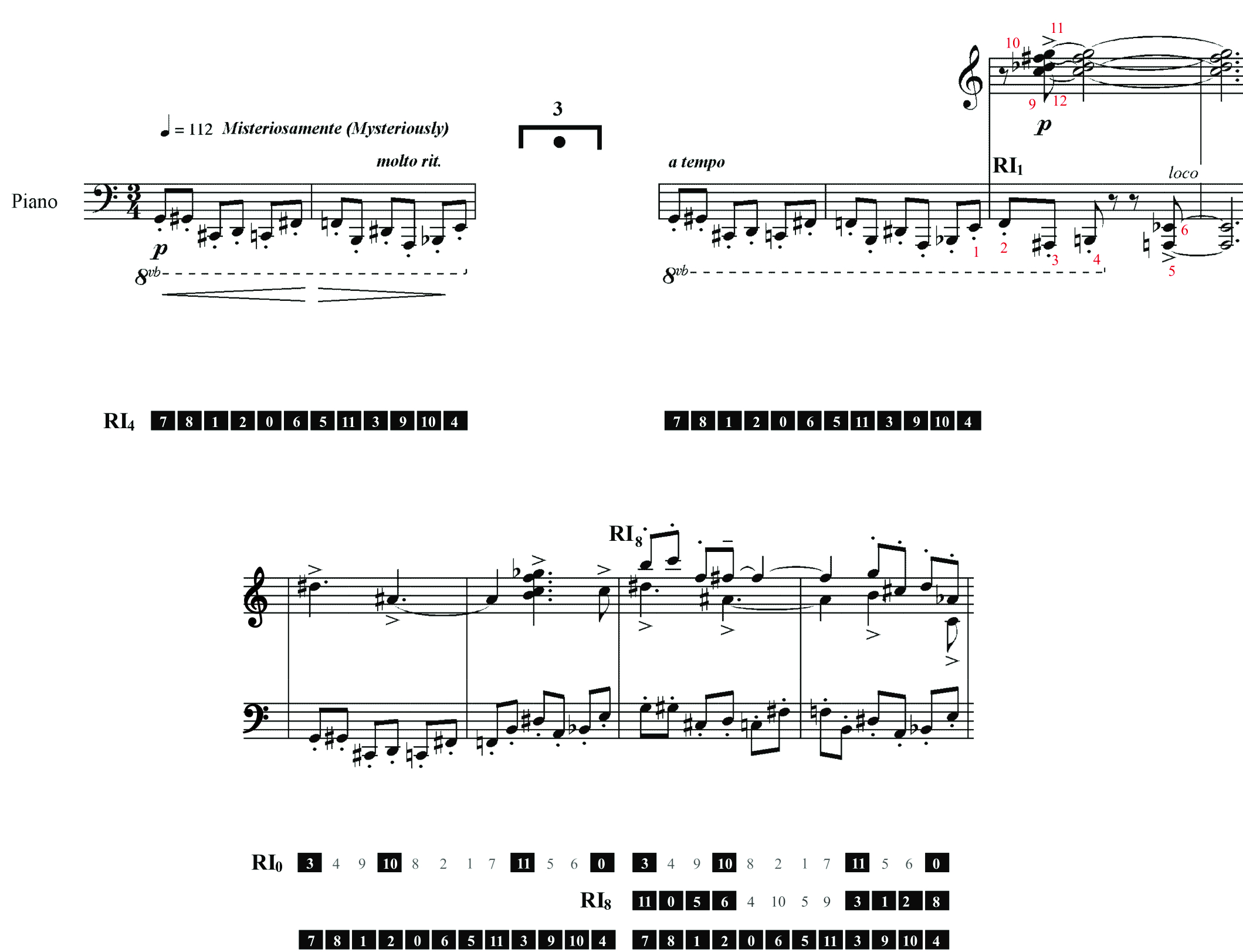
Figure 3. Construction of the Set performed through time
Another gesture, shown in Figure 4, is a spatial metaphor of the Cantor Set; it has three segments: the first is identical to the third and the middle one is replaced by the lowest cluster of the piano. The pitches of first and third segments are organized symmetrically around the axis F and the way they unfold through time to reach a tritone also have some degree of similarity with the process of removing the middle part of a line. Vertical rows with the middle part removed and melodic fragments created by the interpolation of a middle pitch within the generative tetrachord 0167 are also devices used to depict the Cantor Set. Figures 5 and 6 illustrate these devices. Whereas, in Figure 7, a potential middle cluster is replaced by silence against an ostinato in the background, in Figure 8 the same ostinato represents the continuous line and two octatonic tetrachords separated by silence represent a line with a removed middle segment. One should notice that this tetrachord is formed by the removal of the middle pitch of a chromatic pentachord (B, C, C#, D, Eb), also a gesture related to the formation of the Cantor Set.

Figure 4. Lowest cluster framed by an unfolding tritone

Figure 5. Vertical row with removed middle segment

Figure 6. 0167 fragment with interpolated middle pitch

Figure 7. Ostinato and fragments of clusters

Figure 8. Ostinato and octatonic tetrachord
A gesture that offers a better representation of the geometry of the Cantor Set is shown in Figure 9. Since the diagram is too large, we will drawn its general contour and magnify a small region in order to examine its internal pitch structure.
The twelve tone rows are employed in four rhythmic levels. The slowest level uses RI8 applied to twelve groups of three dotted half notes. The second slowest level uses RI0 applied to dotted half notes. The next level uses R0 applied to quarter notes and the fastest level uses P0 applied to eighth note triplets. Each twelve tone row is separated by a segment of rests with the same length of the row. These rests represent the removed middle segment of the Cantor Set. Therefore, this process is a literal drawing of the Set in the domain of space. The reiteration of the same rows over and over helps the listener to identify the similarity between the melodic lines and thus to build an aural representation of the geometric design of the Cantor Set across the work’s duration. In the last gesture of the piece, shown in Figure 10, the same twelve tone row used at the very beginning gradually disappears, serving as a metaphor for the dissolution of a line into dust.
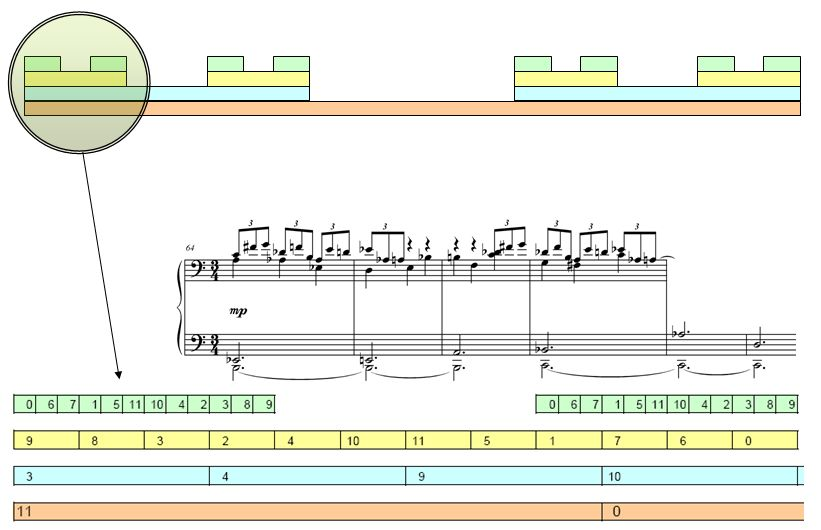
Figure 9. Literal representation of the Set in the dimension of space

Figure 10. Last gesture of Pó
We have described the connections between the design of Pitombeira’s Pó and the Cantor Set. This geometric structure can be considered the basis for a compositional system capable of yielding several designs and, consequently, a large number of pieces. The construction of this piece also inspires us to use the infinite resources of math as the basis for compositional gestures and as models for analytical studies.
References
Erickson, Robert. “Time-Relations”. Journal of Music Theory, Vol.7, No.2 (Winter 1963), 174-192.
Isaacson, Eric J. “Similarity of Interval-Class Content Between Pitch-Class Sets: the IcVSIM Relation.” Journal of Music Theory, V.34/1 (Spring 1990): 1-28.
Solomon, Larry. The Fractal Nature of Music. Available at http://solomonsmusic.net/fracmus.htm. (3 October 2009)