Pedra Mística — for symphonic orchestra, 4 vocal soloists and choir — Interaction of structure, materials and expressive content through the Golden Proportion
Antônio Carlos Borges-Cunha – [email protected]
Universidade Federal do Rio Grande do Sul
This article reports the compositional process of Pedra Mística for symphonic orchestra, four vocal soloists and chamber choir. The piece was written in 1994-95 as part of my research at the University of California, San Diego toward the development of a conception of large form and the elaboration of a method to generate and organize musical materials at all structural levels. Both the macro-forms and the micro-events are organized according to the proportions of the Golden Section and the Fibonacci numerical sequence. This is also true of local rhythmic activities and the pitch content. However, my intention has been to create artistic expression through sound experience, and to seek emotional depth, rather than simply being faithful to compositional systems. There are no completely rigorous realizations of pre-compositional schemes in this work. The main function of the systems and methods was to stimulate the compositional imagination and to suggest possibilities which might not otherwise be considered.
The title of the composition is taken from the poem Pedra Mística which serves as the text set in the second large section of the piece. The poem and its respective translations into English and Italian are reprinted with the permission of its author, the Brazilian writer Libério Neves.
A brief theoretical introduction is given, along with a structural analysis of the piece, from the standpoint of the application of the methods used in the compositional process.
Key words: compositional process, temporal proportion, golden section proportion, Fibonacci numerical sequence, music and poetry.
Introduction
The development of a conception of a large form and the elaboration of a method to generate and organize musical materials at all structural levels has been at the center of my research for many years. In my early works, I avoided the principles of linear continuity and cause and effect at the middle and large scales. The large forms, in fact, were never planned in advance: they resulted from a collection of short segments articulated mostly by expressive silences. Since 1991, when I started working on Ancient Rhythms for string orchestra, 4 clarinets and 5 percussionists my aim has been to integrate apparently opposing conceptions of time and continuity, such as: linearity vs. non-linearity, cause and effect vs. unexpected reaction, climactic vs. anticlimactic, static vs. dynamic. The compositional process, instead of starting at the micro gestural level, involved a careful plan for the overall dramatic shape of the piece, as well as a clear definition of the basic musical materials.
In Pedra Mística1, both the macro forms and the micro events are organized according to the proportions of the Golden Section and the Fibonacci numerical sequence. This is also true of local rhythmic activities and the pitch content. However, my intention has been to create artistic expression through sound experience, and to seek emotional depth, rather than simply being faithful to compositional systems. There are no completely rigorous realizations of precompositional schemes in this work. During the compositional process, the main function of the systems and methods was to stimulate my musical imagination and to suggest possibilities which might not otherwise be considered.
The title of the composition is taken from the poem Pedra Mística which serves as the text set in the second large section of the piece. The poem and its respective translation into English and Italian are reprinted with the permissions of its author, the Brazilian writer Libério Neves (see text on page 8). Both the evolutionary continuity and sonorous world of the piece are in sympathy with the poem. The words Pedro, padre and pedra bestow an immediately religious connotation to the text. They are reiterated and echoed throughout the entire poem. The ritualistic strength, the articulative stress and the reiterations of these words suggested the idea of brass instruments, vertical blocks of sound, and the dramatic contrasts which dominate certain sections of the piece (e.g., the sudden revelation of an off-stage choir which I call “Motet I” at measure 146).
The text discloses a staged evolution (“conceded, wins, conceived, bears, shaped, grows”) and dissemination or ramification (“conceiving, shaping”) followed by the most natural and, probably, the most undesired transformation (“putrefied”). The temporal progress of the text proposes an evolutionary musical texture which starts at a low, yet intense, level of information and moves on to rather complex contrapuntal passages.
No less important is the spatial design of the poem which suggests antiphonal behaviors. The first line of the poem is symmetrically distributed from the left to the right edges. In the second line, there is an empty space between the verb concedeu and the conjunction e; in the third and fourth lines the article a and the noun pedra are isolated on the right edge; in the fifth line, the verb vence is placed at the left edge followed by an empty space, and so on. The above elements, when interwoven, led to the treatment of boundary conditions of blocks and to the use of expressive silences in the music.
I. Rationale
Although the remarkable properties of the Golden Section proportions and their connections with the Fibonacci series are vastly documented in the literature, some explanation of those interrelated characteristics are given here. The rationale is based on Huntley’s The Divine Proportion: a study in mathematical beauty and Krammer’s The Time of Music.
The Golden Section (henceforth GS) occurs when a distance or musical time is divided in such a way that the proportion of the whole to the larger part corresponds to the proportion of the larger to the smaller part. Huntley (1970) mentioned that in the beginning of the twentieth century, it was suggested that the Greek letter ø (Phi) - the initial letter of Greek sculptor Phidias’s name - should be adopted to designate the golden ratio. This proportion can be obtained if and only if the whole is divided at the GS point. The value of the ratio is irrational: if the full distance or the entire segment of musical time constitutes the unity, the larger portion approximates to 0.618034…; the small portion approximates 1.618… For example, the GS a musical segment of 144 units of time is at unit 89, resulting from the multiplication or from the division of 144 by the GS ratio:
Let a line AB of length 1 be divided into two segments by the point C (fig. 1). If C is a point such that 1:AC as AC:CB, then C is the “golden cut” or the golden section of AB. The ratio 1/AC or AC/CB is called the golden ratio.

Figure 1. The Golden Section
The same proportions may be applied to the internal divisions and sub-divisions of each part, generating a hierarchy of interlocking relationships. It is important to observe that the large portion of each partition may be followed or preceded by the short one; that is, the positioning of the parts is variable. For practical reasons, Erno Lendvai, in his studies of Bartok’s music, calls the larger portion positive (0.618) and smaller negative (1.618). In Fig. 2, C is the GS of AB; D is the GS of AC, but it is also the GS of entire length AB in the reverse direction. Similarly, E is both the positive GS of DB and the negative GS of CB; F is the positive GS of AD and the negative GS of AC. Furthermore, the system can be extended or contracted in both directions with similar results. The possibility of multiple interlocking relationships based on the same ratio is the salient characteristic of the GS division, and certainly, this explains its ancient and pervasive importance in architecture, painting, sculpture, music, and science. In fact, the process of reflecting the whole into smaller parts, and vice-versa, relates to the principles of self-similarity and fractal-geometry.
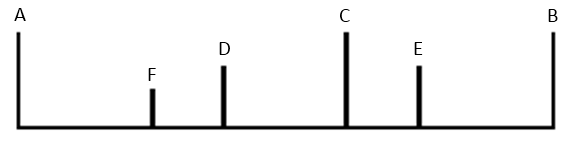
Figure 2. Positive/Negative Partitioning of Golden Section
The Golden Section is closely connected with the Fibonacci sequence which is an additive series formed according to the rule that each term after the second is the sum of the two preceding terms.
…
The ratio of two consecutive terms approximates more and more closely to GS as the numbers increase. That is, the ratio of the ascending Fibonacci sequence moves closer and closer to the value of 0.618… or 1.618… The approximations oscillate, being alternately greater than and less than the irrational value of the GS:
1/1 = 1 1/1 = 1
1/2 = 0.5 2/1 = 2
2/3 = 0.666... 3/2 = 1.5
3/5 = 0.6 5/3 = 1.6661
5/8 = 0.625 8/5 = 1.6
8/13 = 0.6153846 13/8 = 1.625
13/21 = 0.6190476 21/13 = 1.6153846
21/34 = 0.617647 34/21 = 1.6190476
34/55 = 0.6181818 55/34 = 1.6176471
55/89 = 0.6179775 89/55 = 1.6181818
89/144 = 0.6180555 144/89 = 1.6179775
144/233 = 0.6180257 233/144 = 1.6180556
233/377 = 06180371 377/144 = 1.6180258
377/610 = 0.6180327 610/377 = 1.6180371
610/987 = 1.6180344 987/610 = 1.6180328
For my expressive and aesthetic intentions in some of my compositions, the relevant characteristic of the Fibonacci series include:
The intimate connection with the GS proportion. As demonstrated above, the Fibonacci sequence relates directly to the GS. However, it is a more manageable way of expressing and working with the irrational value of a GS partitioning, since it constraints its values to integers.
The implication of natural growth. Although the Fibonacci sequence is not an arithmetic series. ( 1, 2, 3, 4, 5, 6,…) nor a geometric series (1, 2, 4, 8, 16, 32,…), it has characteristics of additive process and of natural organic growth, since it is a additive series and the only one associated with the GS proportion.
Aspects of both predictability and irregularity. The Fibonacci sequence can support the symmetric characteristics of the GS, as indicated above. However, it is also seemingly irregular, since any two successive terms of the sequence have no common divisor other than 1, and they seem to grow in a puzzling, non-predictable way.
The Fibonacci sequence, therefore, allows compositional systems to integrate formal balance, order and flexibility. In other words, the Fibonacci series facilitates the application of the GS proportions in music composition, being a tool for different aesthetic claims, including the interlocking of order and entropy.
II. Analysis
Formal Design
Although Pedra Mística consists of one single large movement, it may be divided into four major parts, according to the GS proportion found within the Fibonacci (henceforth F) numerical series. The approximated proportions are calculated in units of time, considering that the time signatures (measures) are irregular.
- Part I: from the opening (F0) to measure 78 (F233)
- Part II: from measure 78 (F233) to measure 127 (F377)
- Part III: from measure 197 (F377) to measure 197 (F610)
- Part IV: from measure 197 (F610) to the end (F987)
Figure 3 shows that the main structural boundaries of the composition coincide with large numbers of the Fibonacci sequence (henceforth F) which represent unit of time in beats. The beginning of the second part (voice entrance - measure 78) coincides with F233; the vocal climax and the beginning of the orchestra tutti (vertical blocks - measure127) occur at F377; the beginning of the last large section, measure 197, coincides approximately with F610, after Motet I (second offstage choral intervention). Each structural point functions both as positive and negative GS in relation to different structural boundaries, including the internal sectional organization2. For example, F233 is the positive GS in relation to F377, and the negative GS in relation to F610; F377 is the positive GS in relation to F610 and the negative GS in relation to the entire temporal structure.
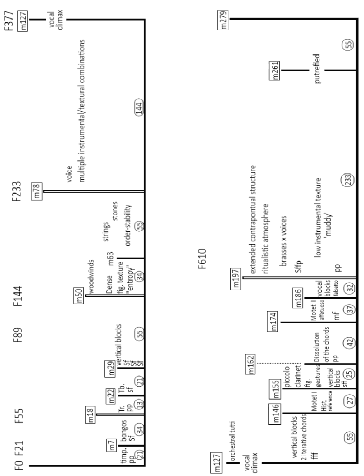
Figure 3. Overall formal layout
Obviously, the numerical proportions do not represent the absolute performance time, since it involves temporal fluctuations, e. g. rallentandi fermatas, and tempo changes, which are not entirely predicted in the structural plan. Temporal fluctuations, however, pertain to the nature of music, and in this case they are essential elements in clarifying the formal design of the work. In fact, I understand our perception of musical time as stimulated by these alterations of the temporal flow.
The first part functions both as an orchestral introduction and as a non-verbal realization of the sonic images and temporal progress suggested by the poem, figure 4.

Figure 4: The text: Poem by Libério Neves
The relatively long orchestra introduction consists of 233 time units. Its most significant textural contrast occurs at the GS partition F144, measure 50, which marks the beginning of a dense figurative woodwind texture. The staged evolution of the text (“Conceded, Wins, Conceived, Bears, Shaped, Grows…”) proposes an evolutionary musical texture. This evolution is disseminated and ramified (“Conceding, conceiving, Shaping, Obscured) and finally arrives at a natural, but undesirable transformation: “putrefied”. All the important steps of the textural construction, which begin from almost nothing and move toward rather complex contrapuntal passages, coincide with the GS partitions. For example, the down-beat of measure 7, where the bongos are added, corresponds to F21. At measure 18, F55, the trumpets, pp legato, initiate the second section of the introduction: 13 beats late, (m.22) the trombones introduce the sfp gestures which lead to the vertical blocks sffp starting at measure 29 (F89 ), figure 5 (pages 13-16).
Similar to the interconnected proportions of the overall form of the piece, each internal partitioning of the introduction functions both as positive and negative GS in relation to different structural points of the piece. Measure 18 (F55) is the negative GS in relation to measure 50 (F144) and the positive GS in relation to measure 29 (89). As already mentioned, measure 50 (F144) is the positive GS of the entire introduction. However, it is also the negative GS in relation to measure 127 (F377, vocal climax, orchestral tutti). This is an example of parallel reflections in the large form. The horizontal lines of the woodwind texture (at the negative GS of the time between F0 and F377) are answered by vertical blocks much latter in the piece (at the positive GS of the time between F0 and F610). Notice that F610 marks approximately the beginning of the last large section, part IV, the most contrapuntally complex in the work.
In the sections of the piece following the introduction, the internal structure becomes much more flexible, because of the influence of the texts formal design and its possible expressive arguments. Only the most significant structural boundaries coincide numerically with the GS proportions. Nonetheless, most of the internal partitions are taken as opportunities to explore both the meanings and sonorities of important words of the poem. Measure 108, for example, represents numerically the positive GS in relation to the beginning of the second part (from vocal entrance, measure 78) to the vocal climax (measure 127). In this case, the thinned out texture associated with the numerical proportion of m. 108 serves to emphasize the word “nasce” (“bears”) at measure 110.
The beginning of Motet I (m.146 ) and Motet II (m. 174 ) coincide with internal GS partitions in relation to their surrounding instrumental sections. Measure 146 is the negative GS in relation to the length between the onset of the orchestra tutti (vertical blocks m. 127 ) and the beginning of the Motet II (m.174 ) which is also the positive GS between Motet I and the ending of the third large section of the entire piece (m. 197). It is important to mention that the length of all these internal structural points just approximates the GS partitions. However, “imperfections” are essential elements in generating and emphasizing dramatic expression, specially at the middle and local level. With Motet I, for example my intentions are:
- To introduce an apparently unrelated musical word. Pure vocalism and textural simplicity intensify the contrast in relation to the preceding and following orchestral tutti.
- To clean out the texture and prepare the listener for a new important word in text’s progress—“ alvoreceu” (“emerged”).
- To explore pure phonetic qualities of language, which are less present in the previous lines of the poem (vowels o and u). Notice that the diphthong eu is separated into two syllables; the purpose of this separation is also to balance the phonetic qualities of the passage.
Phenomenologically, Motet I may be understood as another manifestation of the pauses and fermatas that separate the intense vertical blocks of the previous subsection. Its staticism, textural simplicity, and historical reference to the musical style of the early Middle Ages conveys a virtual religious universe.
Motet II, measure 174-195, is prepared by a gradual dissolution of the orchestral tutti and its vertical blocks of sound (chords) The instrumental chords lose their intensity and are ultimately transformed into a polyphony of vocal lines. Notice that Motet II divides into two segments, but the partitioning does not follow the GS mathematical proportions, resulting instead from my interpretation of lines 18-23 of the poem. In the first segment, the more elaborate texture and caricatured reference to the music styles of the Renaissance and Baroque are insinuated by the words “Tece” (“weaves”) and “Prece” (“Prayer”). Similarly, the melismas on vowels E and A may be understood as manifestations of the empty spaces after a single capitalized vowel, lines 18 and 20, as well as after a single word, lines 19, and 21. My intention has been to project some of the multiple and intensive meaning implied by the emptiness of these poetic lines.
Metric Organization and Local Rhythmic Activity
To organize the metric (time signature) and local rhythmic activities, I prepared matrices to represent the divisions and permutations of a selection numbers of the Fibonacci numbers. For practical reason I have chosen to replace the initial “0” of the sequence with a “1”. Figure 4a and 4b show a selection of Fibonacci numbers, followed by internal divisions manifested in different ways according to a limited permutation principle. (figure 4a and 4b).

Figure 4a. Matrices of Divisions and Permutations of Fibonacci Numbers
Figure 4b is the matrix for the basic rhythmic activities, based on the division and permutations of F55. The roman numbers (I, II, III, IV…) indicate rhythmic cycles used to organize the pre-composition rhythmic scheme.
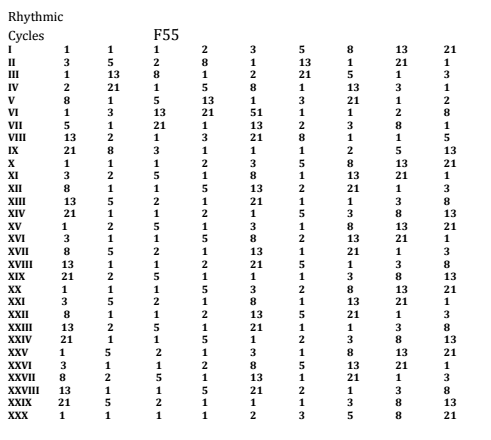
Figure 4b. Matrix for the Basic Rhythmic Scheme
Cycles I, X and XXX represent the original numerical sequence (1 1 1 2 3 5 8…) which is avoided on the local level and used only under special circumstances. Two, three, or four numbers from a permuted Fibonacci sequence can be added or divided to generate other durations not directly related to the sequence. For instance, 8 1 1 5 13 2 1 3 could be also manifested by 9 6 15 4 . The numbers 9 6 15 4 are not in the Fibonacci sequence used in the pre-composition schemes, but they arise from related seeds. This type of arrangement is mostly used for metric organization. For example, the opening phrase of Pedra Mística, measures 1-6, consists of 21 beats: its metric organization derives from the following sequence: 1 1 1 3 2 5 8 . However, for practical and musical reasons, the first three numbers (1 1 1) are summed to make a ¾ bar, and the last number (8) is divided into two 4/4 bars. In the score, the metric organization of bars 1-6 is:
3/4 3/4 2/4 5/4 4/4 4/4 = 21 beats
The local rhythmic are based on the matrix of permutation which represents the internal subdivisions of F55, (figure 4b). The horizontal rows of the matrix (read both forward and backwards) are interpreted as rhythmic cycles of nine attack points using only seven different integers 1 1 1 2 3 5 8 13 21. These numbers are used as multipliers for basic units such as eight-notes, triplets, sixteenth-notes, quintuplets, and sextuplets.
Using the permutations provided by the matrix, figure 4b, I composed the rhythmic skeleton for the entire piece. That is, the possible rhythmic scheme of each section was always written first on graph paper. There, the metric organization was not yet defined, and its definition depended on more concrete musical realization. It is only a potential rhythmic scheme that stimulates and organizes the musical imagination, allowing improvisational gestures. Figures 5a, 5b, 5c and 5d show the basic rhythmic scheme of the first 67 measures of the score. The beginning of cycles are indicated with O and roman numbers. As mentioned before, the graphic paper do not present the metric organization (time signature); it is just a rhythmic skeleton written in 4/4 to facilitate the synchronization of superimposing cycles. The metric is decided with creation of the sounds, gestures and textures during the process of writing and revising the score.
Thus, in conclusion: in my compositional process, the final version of the score results from many versions of the same idea. Frequently, the process of writing different versions for each idea stimulates creativity, suggesting solutions that could be distant from the initial concept.
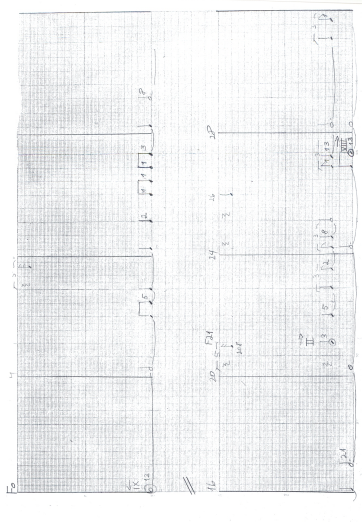
Figure 5a: Basic Rythmic Scheme, measures 1-10. overall formal layout

Figure 5b: Basic Rythmic Scheme, measures 11-20. overall formal layout

Figure 5c: Basic Rythmic Scheme, measures 21-31. overall formal layout

Figure 5d: Basic Rythmic Scheme, measures 40-49. overall formal layout
Originally, the piece started with just one rhythmic line calculated and presented in eighth-notes, the retrograde of the rhythmic cycle IX of the F55 matrix (timpani quintuplets and woodwind figurative gestures were added later). Cycle IX is followed systematically by cycles VIII, VII, VI, V, and so on. At F21 (bongos, m.7 of the score), a new layer of rhythmic is stated, calculated in triplets. It corresponds to the rhythmic cycle II of the matrix of permutation and is followed by cycles III, IV, V, and so on. In this stage, once the procedure and rules are set for each section or segment of the piece, the preparation of the material is systematic.
A further rhythmic layer is added at F55 (trumpets - measure 18), calculated in sixteenth-notes (figure 5b). This particular one starts with the cycle I; that is, the line one of the rhythmic matrix, presenting the original sequence, 1 1 1 2 3 5 8 13 21. Cycle one is followed systematically by cycles II, III, IV etc. At measure 22, the trombones initiate one more rhythmic layer, calculated in quintuples (fig. 5c). From this point to the end of the first section of the piece (m. 49), the main musical substance operates exclusively with these four rhythmic lines under the following basic constraints:
- Trumpets focus their activity on lines 2 and 3 of the rhythmic scheme (triplet and sixteenth-note units);
- Trombones combine line 4 and 1 (quintuplet, and eight-note unit);
- Horns participate as collaborators across all four lines.
Figurative Interventions
From the very early stages of the compositional process, I planned to have aperiodic and unexpected figurative interventions through out the first section of the piece. The character and material of the interventions would have to be extremely independent of the main musical substance. The figures were to have two basic functions:
- To incorporate the idea of contrast between apparently unrelated worlds;
- To foreshadow the main substance and characteristics of future events.
Although these intervening gestures were composed intuitively or derived from fragments of future events or sections, their starting points were all pre-calculated by multiplying the numerical sequence of the already determined rhythmic cycles by the factor 2. 6. Two cycles are superimposed — cycles II and IX of the matrix. On the graph paper, the two cycles are differentiated by the position of the heads or directionality of the stems, indicating the moment to start a figurative intervention or a orchestra sound that is not part of the local texture yet. Here are some examples: the flute gesture starting at the end of measure 3; the wood-wind chord, sfp at the end of measure 6; the wood-wind figure in measure 9.
Other Ways of Interpreting the Rhythmic Schemes
The larger numbers of the matrix — 13 and F21 — were thought of a special durations whose content could be interpreted in different ways, such as:
- Sustaining sounds
- Short attack followed by long rest
- High activity throughout
Therefore, the long values of the rhythmic scheme may act as a reduction of activity or as opportunities to substantially increase the density of attacks. The dense woodwind figurative texture, measure 50 - 62, is partly based on reinterpretation of the rhythmic scheme, the four top lines of figure 5d. One may observe in the score that the most intensive gestures of this passage correspond to the long values of the rhythmic scheme. It may also be understood as one musical interpretation of the spatial design of the poem. The empty spaces between the lines, as well as the empty space that precedes or follows isolated vowels or words are, in fact, replete meanings, and are open to multiple interpretations.
Pitch Content
To define the basic pitch content, I experimented with translating the same numerical proportions of the large form and rhythmic scheme into a sequence of pitches and intervals. This involved a very simple operation: the distance between the Fibonacci numbers was translated as pitch intervals calculated in semitones.
| 0 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
| C | C# | D | D# | F | G# | C# | A | A# | G | F | C | F | F | Bb |
One of the positive aspects of this sequence is the weight given to specific pitches. The sequence consists of fifteen notes, but there are only nine different pitches: E, F#, and B are not present. Observe that on this pitch level (transposition) F repeats 4 times (primary pitch center); C repeats 2 times (secondary pitch center); and C# 2 times (secondary pitch center). The weight given to specific pitches was also understood to reflect the reiteration of certain phonetic patterns of the poem: “Pedro — padre — pedra; concedeu — concebeu — alvoreceu”.
Basic Constraints for Using the Pitch Material
- The basic pitch sequence is not used as a series of fixed intervals, but as a kind of mode. I prepared a matrix with a limited number of rows (21), using the same permutational principle as the numeral duration (figure 6);
- A mode could be transposed to any pitch level;
- Two or more transpositions may be operating simultaneously;
- The predominant note, resulting from a chosen transposition, could function as a pitch center for the entire texture or as the pitch center for a specific instrumental group. Timbral consistency adds to Pedra Mística’s assertiveness.
- The repeated notes could be substitute for by unpitched sounds (percussion or spoken voice ) or by one of the chromatic pitches not already represented in the chosen transportation of the mode.
The sub-section from measure 18 to 49 illustrates the application of the pitch material. The trumpets, starting at measure 18, project F as the primary pitch center, C and C# are the secondary centers. The initial trumpets’ pitch material is derived from line 2 of matrix. At Measure 22, the trombones interact with line 14 of the pitch matrix, transposed by the interval of a tritone. Thus B, which does not pertain to the trumpets pitch content, is the main pitch center of the trombones; F# and G are the secondary center (F# is also absent from the trumpets’ line). Throughout this relatively large sub- section, C, Bb, and F do not belong to the trombones’ pitch vocabulary. As with the rhythmic activities, the horns participate as collaborators with both the trumpets and trombones’ pitch content. Notice that during the last stage of the sub-section, the trumpets invade the trombones’ area and vice versa. These licenses, both in terms of pitch and rhythm, announce the textual change of the next section (woodwind figurative lines from m. 50), since the lines become more figurative, (e. g. trumpets at measures 40-41).

Conclusion
Pedra Mística was largely organized on the basis of theoretical principals that stimulated the intuition and musical imagination from the large structural level to the micro details. As mentioned in the introduction, my intention has been to create artistic expression through sound experience, and to seek emotional depth, rather than simply being faithful to compositional systems. There are no completely rigorous realizations of pre-compositional schemes in this work. The main function of the systems and methods was to stimulate the sounding imagination and to suggest possibilities which might not otherwise be considered.
The process of describing one’s own creative work can be a tedious experience, but it is, in fact, one more stage in the creative processes as a whole. It helps not only to clarity the present stage of one’s aesthetic values and creative procedures, but also to proliferate ideas to be developed (or avoided) in subsequent projects. It is an opportunity for artists to investigate themselves more fully. Furthermore, although the real value of art is the resulting creative work, a self analysis is the best way to expose one’s ideas and structural procedures to the artistic community, which may also be interested on how a composition is made.
In writing this article, I could have observed closely the connections and disconnections between the initial structural plan, the procedures taken to generate materials, and the final product. For me, compositional systems and methods are not necessary related to mechanical processes, but rather to ways of organizing the musical ideas and generating the musical materials that will then be shaped according to aesthetic criteria. The final score of Pedra Mística resulted from the interaction between the free-flowing imagination and the rational, theoretical basis of the structure. Without the constraining and resistance of the system, most of the musical ideas would probably not have been considered.
References
Borges-Cunha, Antônio Carlos et al. Pedra Mística. Brazil: Universidade Federal do Rio Grande do Sul, 2000. Sound recording.
Huntley, H E. The Divine Proportion: a Study in Mathematical Beauty. New York: Dover Publications, 1970. Print.
Kramer, Jonathan D. The Time of Music: New Meanings, New Temporalities, New Listening Strategies. New York: Schirmer Books, 1988. Print.
Lendvai, Ernö. “Duality and Synthesis in the Music of Béla Bartók.” Hungarian Music Quarterly. 5 (1994): 1-2. Print.
Notes
1 A recording of Pedra Mística is available on the CD referenced at the end of this article or, alternatively, on Youtube: http://www.youtube.com/watch?v=YKBj6Nl8y2E
2 In this analysis, there are numerous references to GS points of symmetry (positive and negative mirroring). While I have not always indicated here the ways in which these correspondence are reflected musically, I invite the reader to examine the score to determine these relationships directly.

